Looking into the nature of the pythagorean theorem.
read moreWe should look at what it means to say a^2 + b^2 = c^2
For instance, how does one of these grow as the other one grows?
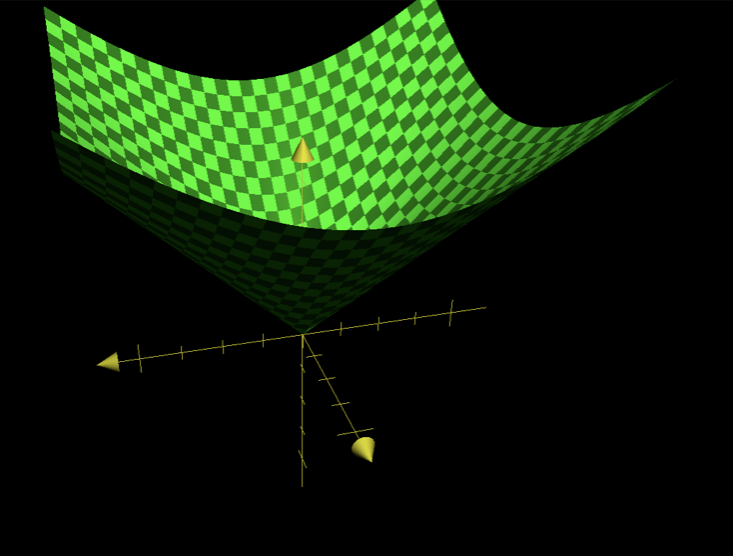
This is the graph of z^2=x^2+y^2
Now, we only want to look at the equation when one of the variables varies (x or y) which is just taking a cross-section of this graph at a given point.
Doing so yields this:
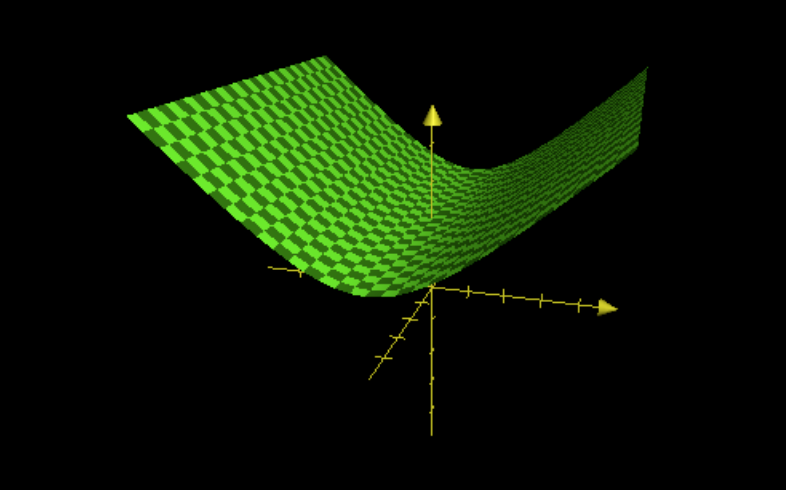
Now that there’s only one variable, we can represent this graph two dimensionally (because all cross sections are equal).
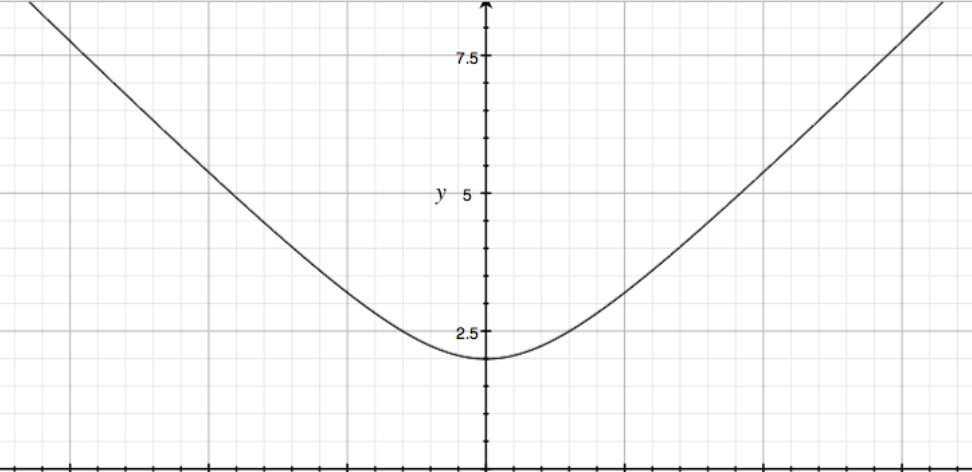
This function appears parabolic near x=0 while it approaches linearity as x goes to positive and negative infinity. Observing the derivative confirms this:
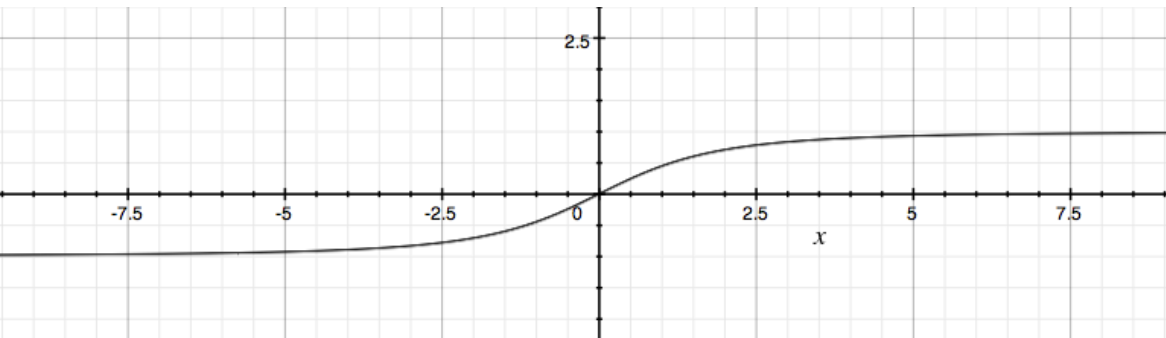
This graph has horizontal asymptotes at y=1 and y=-1. This means it never quite reaches linearity...why? All right, let’s look at this point by point. Well, near the origin, the variation of x isn’t having much of an effect so the value of the derivative is going to be small.
When does x^2+x^2=z^2?
2x^2=z^2